
위와 같은 직각삼각형에서 사인, 코사인, 탄젠트는 아래와 같이 정의된다.

반지름의 길이가 1인 원에서 아래와 같이 삼각형을 그리면
(길이가 1인 단위벡터에서 생각하면)

반지름이 1이므로 x=cosθ , y=sinθ가 된다.

탄젠트는 기울기를 나타내므로 반대로 역삼각함수를 이용해 각도를 구할 수도 있다.
역삼각함수
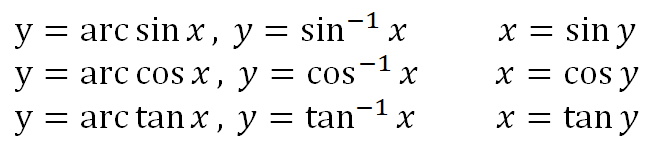
이를 이용해 아래처럼 벡터의 각도를 구할 수 있다.
|
1
|
degree = Mathf.Atan(dir.y / dir.x) * Mathf.Rad2Deg;
|
cs |
dir.y / dir.x = tanθ이므로 역함수에 넣으면 각도인 θ를 구할 수 있다.
결과값은 라디안으로 나오므로 Mathf.Rad2Deg를 곱해주어 60분법으로 바꿀수있다.
'프로그래밍 공부 > 수학' 카테고리의 다른 글
| 내적의 증명 (제1코사인법칙, 제2코사인법칙) (0) | 2019.03.28 |
|---|---|
| 벡터의 내적(dot product) (1) | 2019.03.28 |
| 원주율(Pi)과 라디안(Radian) (0) | 2019.02.23 |
| 벡터 (vector) (0) | 2019.02.23 |
| 선형대수학(Linear Algebra)이란? (0) | 2019.02.23 |



